Numbering Systems
bit = 1 or 0
nibble = 4 bits, half a byte
octet = 8 bits
A byte on most computers is the same as an octet
Binary uses only 1's and 0's
0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000...
Hexadecimal - base 16
Counting: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,10,11,12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B....
A single hex digit = 4 bits/half a byte
Octal - base 8
Counting: 0,1,2,3,4,5,6,7,10,11,12, 13, 14, 15, 16, 17, 20...
Decimal - base 10
Counting: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20...
Place value is the key.
In decimal our BASE is 10:
BASE ^ 0 = 10^0 = 1, "ones"
BASE ^ 1 = 10^1 = 10, "tens"
BASE ^ 2 = 10^2 = 100, "hundreds“
A number like 25 is broken down:
(2*10) + (5*1) = 20+5 = 25
In hexadecimal the "tens" place is actually "sixteens", and the "ones" stays the same but now consists of 15 numbers, 0 to F.
BASE is 16:
BASE ^ 0 = 16^0 = 1, "ones"
BASE ^ 1 = 16^1 = 16, "sixteens"
BASE ^ 2 = 16^2 = 256, "256ths“
Convert 2A into decimal
(2*16) + (A*1) = (2*16) + (10*1) = 32+10 = 42
Convert Binary to Hexadecimal
(http://www.wikihow.com/Convert-Binary-to-Hexadecimal\
Find a line of up to four binary numbers to convert.
Binary numbers can only be 1 and 0. Hexadecimal numbers can be 0-9, or A-F, since hexadecimal is base-16. You can convert any binary string to hexadecimal (1, 01, 101101, etc.), but you need four numbers to make the conversion (0101→5; 1100→C, etc.). For this lesson, start with the example 1010.
- 1010
- If you don't have 4 digits, add zeros to the front to make it four digits. So, 01 would become 0001.
Write a small "1" above the last digit.
Each of the four numbers signifies a type of number decimal system number. The last digit is the one's place. You will make sense of the rest of the digits in the next step. For now, write a small one above the last digit.
Write a small "2" above the third digit, a "4" above the second, and an "8" above the first.
These are the rest of your place holders. If you're curious, this is because each digit represents a different power of 2. The first is 2^3, the second 2^2, etc.
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
Count out how many of each "place" you have.
Luckily, this conversion is easy once you have four numbers and know what they all mean. If you have a one in the first number, you have one eight. If you have a zero in the second column, you have no fours. The third column tells you how many twos, and the second how many ones. So, for our example:
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 8 | 0 | 2 | 0 |
Add your four numbers together.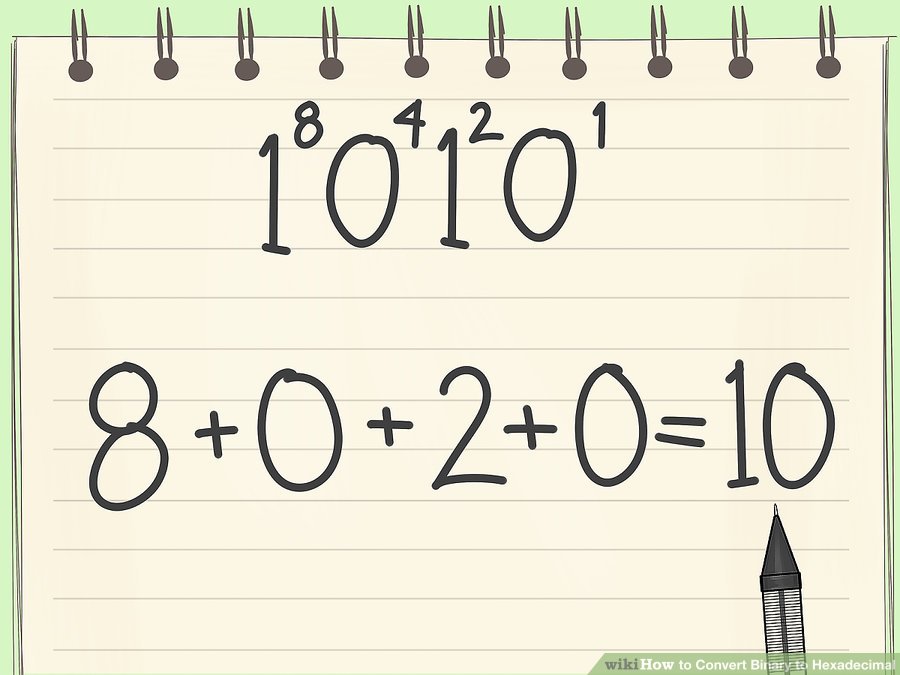
Final answer:
The Binary number 1010 converts to A in the hexadecimal system.
| Bin | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dec | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Hex | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A |
For long binary strings, break them up into groups of 4. Add extra zeros to the front of the first number if it is not four digits.
The zeros will not affect the conversion, but they will make it easier to visualize. Remember, you want all groups of 4-digit binary numbers.
- Convert 11101100101001 into a hexadecimal number.
- 11101100101001 = (11)(1011)(0010)(1001)
- (11)(1011)(0010)(1001) = (0011)(1011)(0010)(1001)
Convert one 4-digit group at a time.
You'll need to convert each binary set by itself, so separate them on your paper to make them easier to work with. Work on converting each individual string of four into its hexadecimal counterpart. For our example: 0011
- 0011 = 0+0+2+1 = 3
- 1011 = 8+0+2+1 = 11 = B
- 0010 = 0+0+2+0 = 2
- 1001 = 8+0+0+1 = 9
Remove the spaces to create your hexadecimal number.
Once you've converted all the 4-digit parts, simply ram them together to get your final answer. So, for the example above:
- (0011)(1011)(0010)(1001)
- 3 B 2 9
- 11101100101001 = 3B29
Convert long binary string to Decimal
| 8192 | 4096 | 2048 | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
- 11101100101001 = 15,145